I'm having a little trouble putting this together. I believe I have the formula correct on the bottom, but I can't seem get the program to work. The idea is that it needs to be able to run like this:./sdev in concept, but not.
The uniform distribution is used to describe a situation where all possible outcomes of a random experiment are equally likely to occur. You can use the variance and standard deviation to measure the “spread” among the possible values of the probability distribution of a random variable.
For example, suppose that an art gallery sells two types of art work: inexpensive prints and original paintings. The length of time that the prints remain in inventory is uniformly distributed over the interval (0, 40). For example, some prints are sold immediately; no print remains in inventory for more than 40 days. For the paintings, the length of time in inventory is uniformly distributed over the interval (5, 105). For example, each painting requires at least 5 days to be sold and may take up to 105 days to be sold.
The variance and the standard deviation measure the degree of dispersion (spread) among the values of a probability distribution. In the art gallery example, the inventory times of the prints are much closer to each other than for the paintings. As a result, the variance and standard deviation are much lower for the prints because the range of possible values is much smaller.

How to write a C Program to Calculate Standard Deviation, Mean, and variance with an example? Before this example, we have to understand a few concepts, such as Mean and Variance, before understanding the Standard Deviation. Standard deviation can be difficult to interpret as a single number on its own. Basically, a small standard deviation means that the values in a statistical data set are close to the mean of the data set, on average, and a large standard deviation means that the values in the data set are farther away.
For the uniform distribution defined over the interval from a to b, the variance equals
The standard deviation is the square root of the variance:
For example, the variance of the uniform distribution defined over the interval (1, 5) is computed as follows:
The standard deviation is:
Standard Deviation Variance Concept
Because the binomial distribution is so commonly used, statisticians went ahead and did all the grunt work to figure out nice, easy formulas for finding its mean, variance, and standard deviation. The following results are what came out of it.
If X has a binomial distribution with n trials and probability of success p on each trial, then:
The mean of X is
The variance of X is
The standard deviation of X is
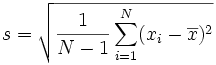
For example, suppose you flip a fair coin 100 times and let X be the number of heads; then X has a binomial distribution with n = 100 and p = 0.50. Its mean is
heads (which makes sense, because if you flip a coin 100 times, you would expect to get 50 heads). The variance of X is
which is in square units (so you can’t interpret it); and the standard deviation is the square root of the variance, which is 5. That means when you flip a coin 100 times, and do that over and over, the average number of heads you’ll get is 50, and you can expect that to vary by about 5 heads on average.
The formula for the mean of a binomial distribution has intuitive meaning. The p in the formula represents the probability of a success, yes, but it also represents the proportion of successes you can expect in n trials. Therefore, the total number of successes you can expect — that is, the mean of X — is
The formula for variance has somewhat of an intuitive meaning as well. The only variability in the outcomes of each trial is between success (with probability p) and failure (with probability 1 – p). Over n trials, the variance of the number of successes/failures is measuredby
Standard Deviation Variance Covariance Correlation
The standard deviation is just the square root.